J’ai découvert au hasard de mes lectures le concept de “mètre étalon des probabilités” (Probability Yardstick 🇬🇧). Il s’agit de définir un ensemble d’adjectifs destinés à refléter différents niveaux de probabilité de façon standardisée. On établit ainsi un langage commun permettant de communiquer efficacement la vraisemblance d’un sujet avec un simple mot. Après tout, “probable”, “possible”, “vraisemblable” ne veulent pas toujours dire la même chose selon qui parle ou dans quel contexte…
Avoir une nomenclature commune est même vital dans certains métiers. En espionnage et renseignement, par exemple.1 Et si il est toujours plus précis de donner un chiffre qu’un mot, faire ainsi rend rapidement l’écoute pénible à l’auditeur.
J’avais déjà rencontré une notion similaire en médecine : quand on parle des effets indésirables, et où on les classe selon leur fréquence en différents degrés de probabilité :
| Mot clef | Probabilité |
|---|---|
| fréquent | Plus d’un cas sur dix |
| Fréquent | Plus de 1 cas sur 100 |
| Peu fréquent | Plus de 1 cas sur 1'000 (103) |
| Rare | Plus de 1 cas sur 10'000 (104) |
| Très Rare | Moins de 1/10'000 |
| Tableau: Appellations de différentes fréquences d’effets secondaires. Source |
Ces fourchettes de probabilité sont assez standardisées dans le domaine des effets secondaires. On en utilise d’autres quand on parle de la fréquence de maladies rares ou de certaines mutation génétiques, d’autres encore en chirurgie…
On peut déplorer ce manque de cohérence, le même mot reflétant différents degré de certitude selon le domaine… Mais les ordres de grandeurs sont d’ampleurs si différentes que c’est malheureusement inévitable.2
Pour revenir au Probability Yardstick : si ce petit bijou de nomenclature semble appartenir aux domaines spécialisés, j’aimerais avoir l’équivalent dans le vocabulaire courant. Ouvrez un dictionnaire, et les définition des adjectifs désignant les probabilités sont au mieux vagues ; et certainement pas hiérarchisées. Une barrière de plus dans nos communications déjà si ardues3. J’ai la conviction personnelle (comprenez : basée sur aucun élément solide4) que la crise du Covid a été si profonde également parce que nous sommes incapables en temps que société de discuter de probabilités et de risques de façon claire.
Je trouve brillant d’avoir ce standard. Je n’ai malheureusement pas trouvé l’équivalent en français… Soit que nous n’en avons pas, soit qu’il existe mais reste trop obscure pour être trouvé facilement. C’est regrettable dans les deux cas : nous aurions tant à gagner d’avoir dans notre langage une façon claire d’exprimer notre incertitude. Au delà d’une preuve d’humilité et de l’importance saine d’un doute raisonnable, notre XVIe siècle en a besoin.
Le cerveau humain subit déjà de nombreux biais quand il s’agit d’estimer les risques567 ; si s’y ajoutent en plus nos compréhensions individuelles de ce que “probable” veut dire, nous allons au devant de longues années de galère…
Si vous, cher·chère lecteur·rice, vous connaissez l’équivalent en français, je serais très heureux de lire vos sources ! Envoyez les moi soit via mastodon (@Jab@piaille.fr), soit par email. Merci d’avance ! 👋
De mon côté, je vais simplement me contenter de traduire et utiliser le modèle britannique. Être cohérent avec moi même me semble être un bon début. Si j’entraîne dans mon sillage linguistique quelques collègues et amis, je serai content.
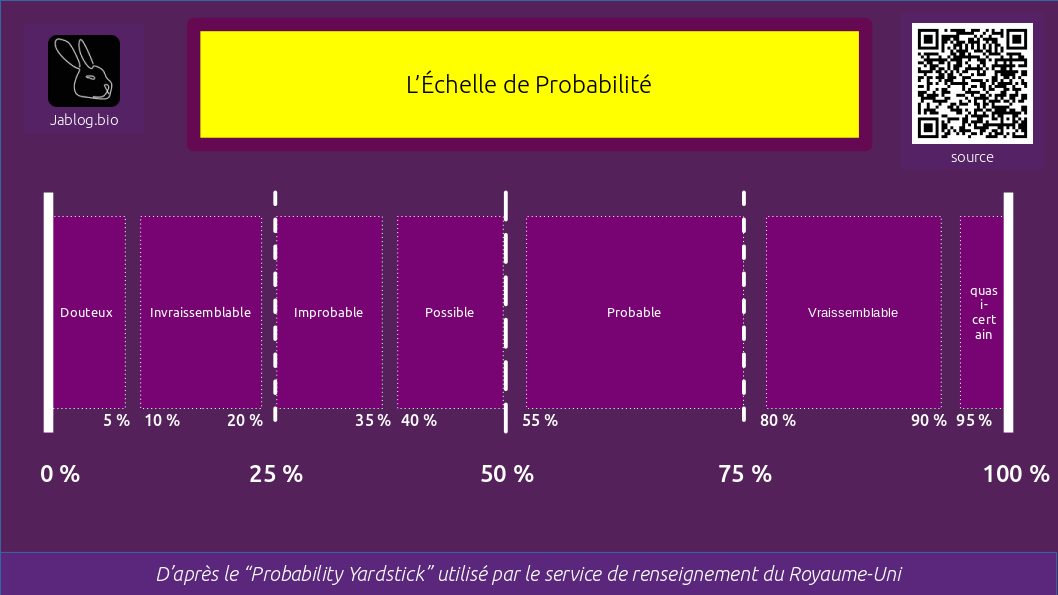
Voici donc l’Échelle de probabilité que je me propose d’employer, honteusement calquée sur le modèle britanique :
On notera que ce spectre est discontinu. C’est fait exprès, d’après les auteurs du modèle source. Ainsi, on ne donne pas une fausse impression d’exactitude des termes : le langage étant forcément moins précis que les maths, il s’agit de donner une idée de la probabilité.
Sentez vous libre de la partager et de la réutiliser. Argumentez pourquoi nous mettre d’accord sur une échelle du risque est si important. Et pensons à préciser nos estimations quand nous changeons de contexte et d’interlocuteur.
-
Defence Intelligence – communicating probability Source 🔗 ↩︎
-
Par exemple, une maladie est rare aux yeux de l’organisme européen Orphanet quand elle touche moins de 1 personne sur 2'000, et fréquente sinon. Source 🔗 ↩︎
-
Il suffit d’une recherche internet pour se rendre compte de la complexité que représente “communiquer efficacement”. Pour les curieux, je propose un point d’entrée : le schéma de la communication de Riley & Riley ↩︎
-
L’intuition n’est pas une preuve. Voir aussi ↩︎
-
Gollier C, Hilton D, Raufaste É. Daniel Kahneman et l’analyse de la décision face au risque. Revue d’économie politique. 2003;113(3):295‑307. ↩︎
-
Martinez F. L’individu face au risque : l’apport de Kahneman et Tversky. Idées économiques et sociales. 2010;161(3):15‑23. ↩︎
-
MILHABET, Isabelle, DESRICHARD, Olivier, VERLHIAC, Jean-François. Comparaison sociale et perception des risques : l’optimisme comparatif. In: Perspectives cognitives et conduites sociales (Vol.8). Rennes : Presses universitaires de Rennes, 2002. p. 215–245. ↩︎